Occam's Razor and Honesty with respect to Beliefs

Consider the following airline passenger data (example courtesy of Wilson et al.):

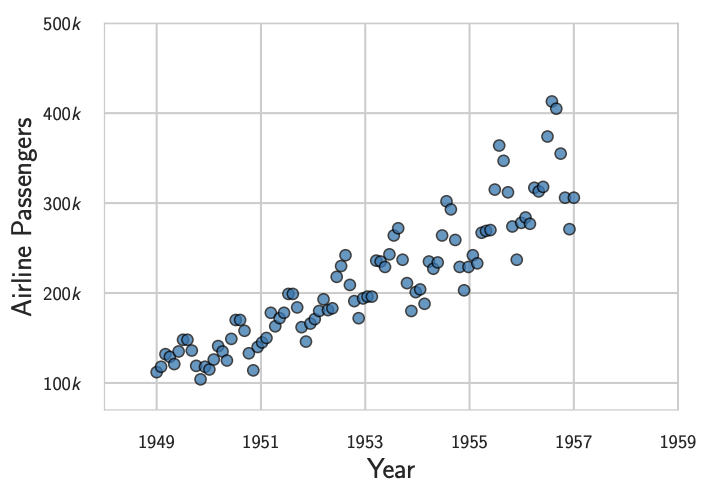
How should we model this data to generate predictions? Suppose we had to choose between two alternative models: $f_1(x)=w_0+w_{1}x$ and $f_2(x)={\sum }_{i=0}^{10^4}{w}_j{x}^j$. The first is a simple linear model with very few parameters while the second is a complex polynomial model with far more parameters. Intuitively, because the data looks linear, of the two models that could both accurately capture the trend of the data, it seems that we should choose the simpler linear model $f_1$. Given two models that both fit the data, we are inclined to choose the simpler one. This is an example of our internalized Occam’s Razor in action. In Information Theory, Inference and Learning Algorithms, Mackay offers a Bayesian probabilistic justification for our intuitive inclination toward simple models.

Mackay

Suppose we have observed data $D$. And let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be two competing models for said data. For a given hypothesis $\mathcal{H}$, we call $P(D|\mathcal{H})$, the probability of the data given model $\mathcal{H}$, the (Bayesian) evidence for $\mathcal{H}$. When we compare and evaluate models, we want to compute $P(\mathcal{H}|D)$, the probability of the model (which represents a hypothesis about the data) given the observed data. The evidence is related to this conditional probability $P(\mathcal{H}|D)$ by Bayes’ Theorem:

$$P(\mathcal{H}|D)\propto P(D|\mathcal{H})P(\mathcal{H}).$$

The $P(\mathcal{H})$ term represents our a priori belief about the hypothesis. We don’t necessarily have to assign any a priori preference for a model through this $P(\mathcal{H})$, that is, we can compare models solely based on their evidence, $P(D|\mathcal{H})$.

The range of data for which $P(D|\mathcal{H})>0$ is true is called the support of the model. Consider the following diagram where we have a conceptualization of all possible datasets on the $x$-axis and evidence on the $y$-axis.

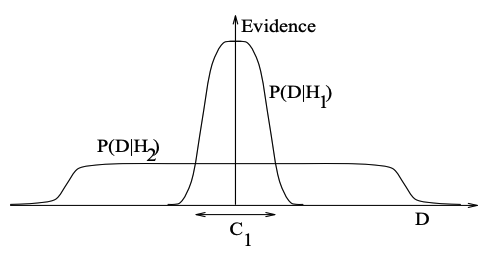
The support for ${\mathcal{H}}_1$ is the region ${\mathcal{C}}_1$. This ${\mathcal{H}}_1$ could be a relatively simple model, such as the linear model from our airline passenger example above. It has limited support, but for datasets that fall into its support, it can assign high evidence. A more complex model such as ${\mathcal{H}}_2$ (eg. the higher order polynomial model from above) will have a larger support since there would be a wider range of datasets compatible with a more complex model. The downside with the more complex ${\mathcal{H}}_2$ relative to the simple ${\mathcal{H}}_1$ is that if $D\in {\mathcal{C}}_1$, then ${\mathcal{H}}_2$ will not be able to assign as much evidence to $\mathcal{D}$ since the probability distribution has to be normalized. This is precisely why the evidence for the simpler model is higher given $D\in {\mathcal{C}}_1$ and thus $P({\mathcal{H}}_1|D)>P({\mathcal{H}}_2|D)$ by Bayes’ Theorem (see Mackay for a more complete explanation).

So, we have probabilistically justified our preference for simpler models given several competing models that all fit the observed data. However, in a paper titled Bayesian Deep Learning and a Probabilistic Perspective of Generalization, Wilson et al. argue that the picture provided by Mackay is incomplete.

Wilson et al.

Consider the following diagram of the data modeling process (from Mackay):

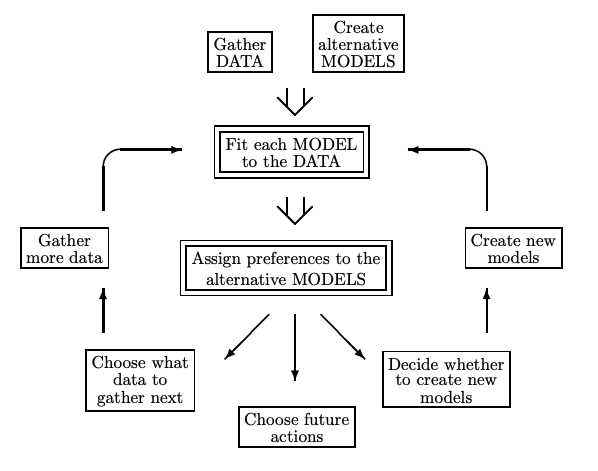
Mackay argues that Bayesian inference can only be used in the two double-framed boxes. Fitting models to data is mostly an optimization problem and the explanation above for Occam’s Razor was more focused on assigning preferences to alternative models. The argument of Wilson et al. boils down to the belief that we should apply Bayesian thinking to the “create alternative MODELS” stage as well. In addition, they are more concerned with the data-generating process as opposed to just the observed data (and in my view, justifiably so).

When we model data, we are not simply concerned with finding some function that approximates the shape of the data. We want to find a function that accurately represents the data-generating process. This is because we want to generate predictions based on our model. And to generate predictions, we need to understand the underlying data-generating function. In the above airline passengers example, while the data looks somewhat linear, intuitively, it seems unlikely that the function generating it is actually linear. This is because we have some a priori beliefs regarding the complexity of the data-generating process. Wilson et al. argue that we are being dishonest with respect to our a priori beliefs about the underlying data-generating process when we choose a linear model based on linear-looking data.

[O]ur beliefs about the generative processes for our observations, which are often very sophisticated, typically ought to be independent of how many data points we happen to observe.

At the very least, we must concede that the underlying data-generating function could be nonlinear. For example, it seems entirely possible that the data-generating function is exponential (in fact, it seems more likely that this is the case) and that we happened to observe the early part of the exponential curve. The point is that we ought not to change our assumptions about the data generating function purely based on the amount of data we observe. Our models should be expressive enough to potentially ‘learn’ any one of our hypotheses about the data-generating process. This expressiveness condition is what justifies our preference for overparameterized models.

The expressiveness condition that Wilson et al. are concerned with can fit into Mackay’s framework at the “create alternative MODELS” stage. To Wilson et al., the creation of alternative models should be solely dependent on our a priori beliefs about data-generating process. We should not decide what models to use after having observed data. This is what it means to be honest about our beliefs. We need to consider whether it is even plausible a priori that the data-generating function is something our model could accurately represent. We want a model that can reasonably describe the ground-level reality. Of course, our knowledge about the data-generating process will never be complete. Otherwise, we wouldn’t really have any need to model the data in the first place¹. However, this doesn’t mean that we shouldn’t incorporate said knowledge into our data-modeling process. In the above airline passenger example, since we have a belief that the data-generating function is complex, we should not even consider the linear model as an option. We should only consider models expressive enough such that it could plausibly capture the complex data-generating function. After all, if we hadn’t seen the linear-looking data, would we have guessed to use a linear model? Probably not. One option for encoding this belief into the Bayesian framework is to use the $P(\mathcal{H})$ term we ignored earlier. We could justify assigning $P(H_1)\ll P({\mathcal{H}}_2)$ by our belief that the data-generating process is complex and will require a complex model to capture it.

Sources:

• MacKay, David J. C. Information Theory, Inference and Learning Algorithms. Cambridge University Press, 2003.
• Wilson, Andrew G., and Pavel Izmailov. “Bayesian deep learning and a probabilistic perspective of generalization.” Advances in neural information processing systems 33 (2020): 4697-4708.

Footnotes

1. For example, with a baseball in free fall, we don’t need to observe and model thousands of instances of baseballs falling in order to predict the trajectory of a falling baseball. This is because we have precise equations that nearly perfectly describe the data-generating process. So, we can generate predictions at ease.) ↩