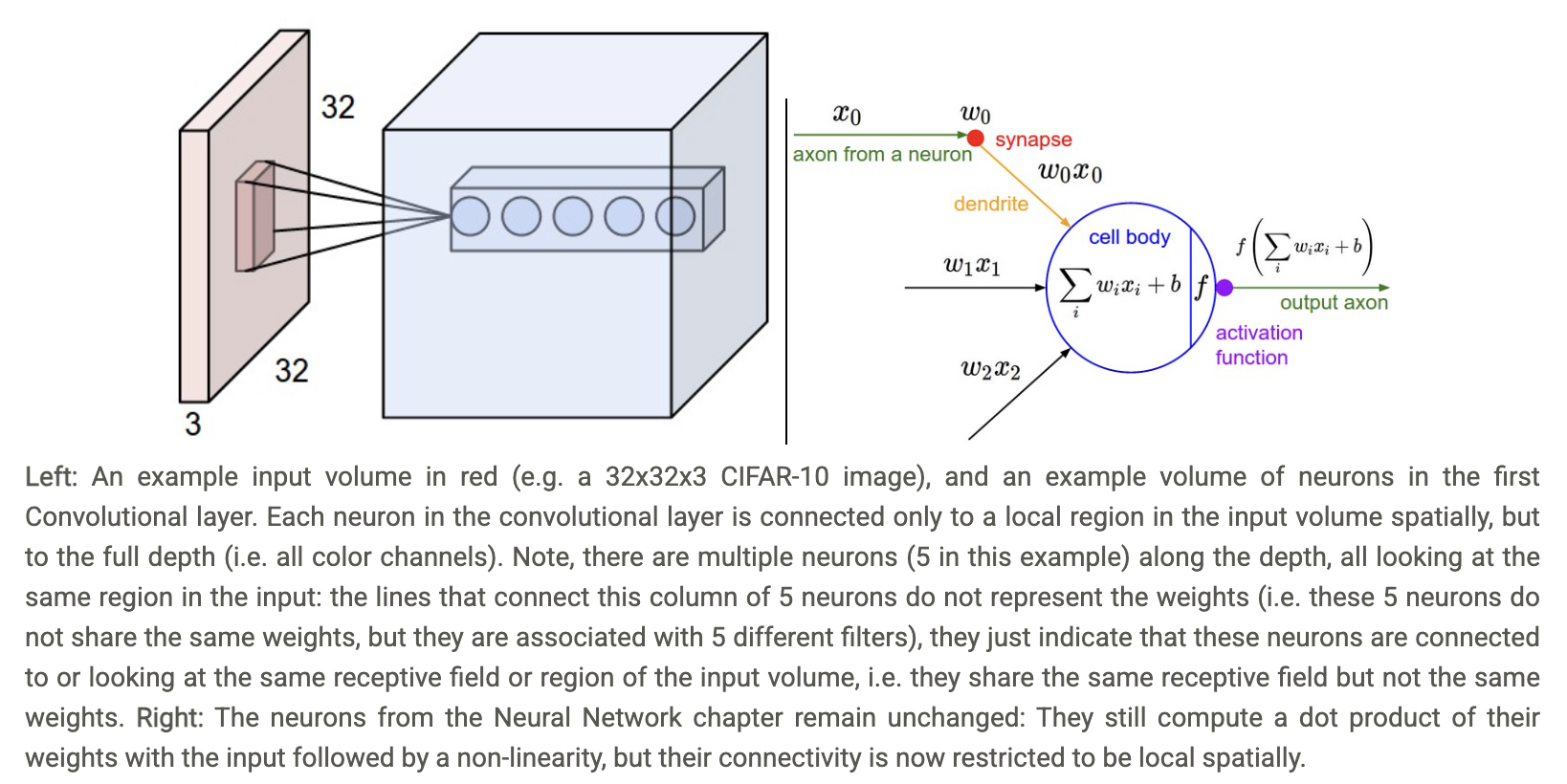
 In the above image, the 5 neurons arranged horizontally represent the ‘width’ of the ConvNet block (aka. number of kernels/filters, channel dimension of output).
In the above image, the 5 neurons arranged horizontally represent the ‘width’ of the ConvNet block (aka. number of kernels/filters, channel dimension of output).
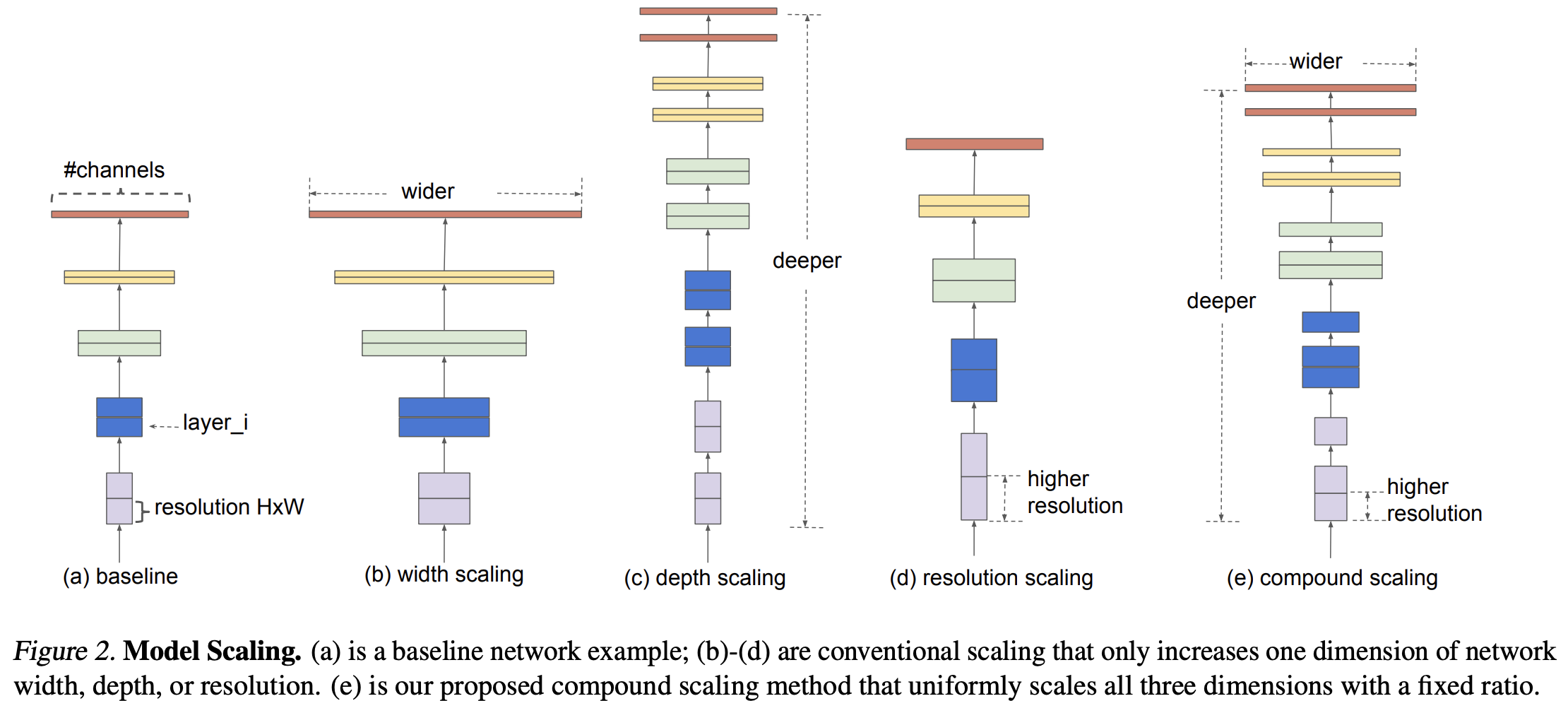
Figure 2 characterizes the 3 main conventional ways of scaling a convolutional networks:
- (b) width scaling: refers to scaling the number of kernels in any given convolutional block
- (c) depth scaling: refers to scaling the number of convolutional blocks
- (d) resolution scaling: refers to increasing the resolution of the input image
The authors propose a new way to scale models: compound scaling (e).
The authors define a ConvNet as follows:
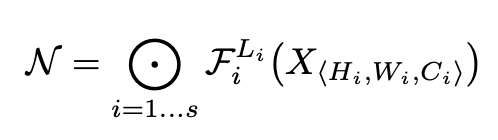 where refers the number of the layer, is the operator, is the input tensor with tensor shape . The superscript of denotes that the layer is repeated times in stage .
where refers the number of the layer, is the operator, is the input tensor with tensor shape . The superscript of denotes that the layer is repeated times in stage .
The intuition for the model scaling problem comes from the following two observations:
Scaling up any dimension of network width, depth, or resolution improves accuracy, but the accuracy gain diminishes for bigger models. In order to pursue better accuracy and efficiency, it is critical to balance all dimensions of network width, depth, and resolution during ConvNet scaling.
The authors formulate the problem of model scaling as such:
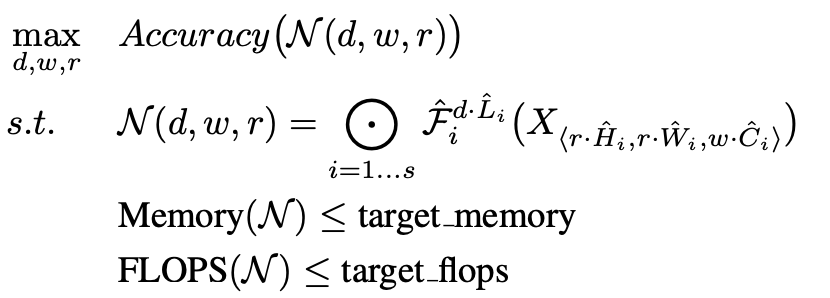
The authors suggest the compound scaling method:
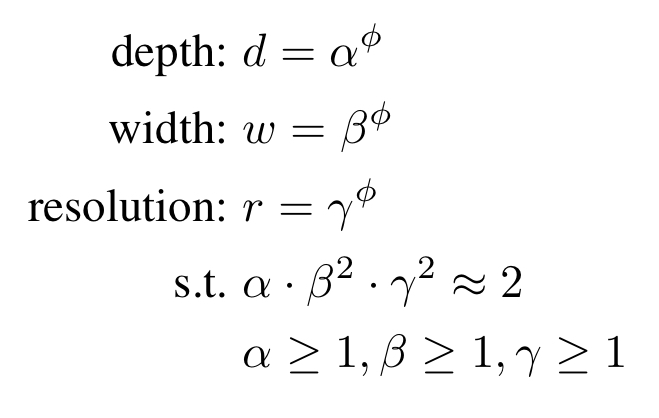
Intuitively, φ is a user-specified coefficient that controls how many more resources are available for model scaling, while α, β, γ specify how to assign these extra resources to network width, depth, and resolution respectively. (…) In this paper, we constraint such that for any new , the total FLOPS will approximately increase by .
Starting from the baseline EfficientNet-B0, we apply our compound scaling method to scale it up with two steps:
- STEP 1: we first fix φ = 1, assuming twice more resources available, and do a small grid search of α, β, γ based on Equation 2 and 3. In particular, we find the best values for EfficientNet-B0 are α = 1.2, β = 1.1, γ = 1.15, under constraint of .
- STEP 2: we then fix α, β, γ as constants and scale up baseline network with different φ using Equation 3, to obtain EfficientNet-B1 to B7 (Details in Table 2). Notably, it is possible to achieve even better performance by searching for α, β, γ directly around a large model, but the search cost becomes prohibitively more expensive on larger models. Our method solves this issue by only doing search once on the small baseline network (step 1), and then use the same scaling coefficients for all other models (step 2).
Resources: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks