ResNet

ResNet

Before ResNet, deep networks would run into the degradation problem where accuracy would get saturated as the number of layers increased, and would start decreasing.

Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error, as reported in [11, 42] and thoroughly verified by our experiments.

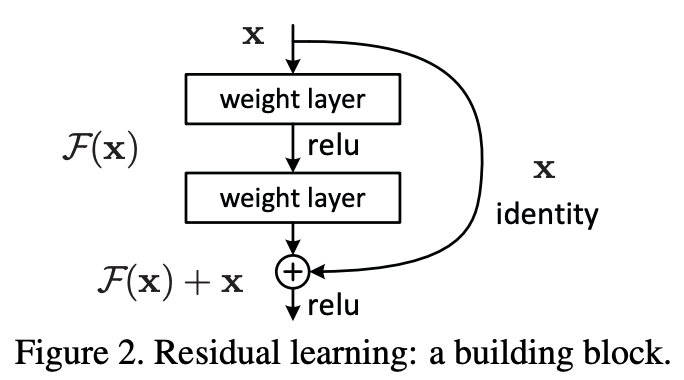
Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping. Formally, denoting the desired underlying mapping as H(x), we let the stacked nonlinear layers fit another mapping of F(x) := H(x)−x. The original mapping is recast into F(x)+x. We hypothesize that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. To the extreme, if an identity mapping were optimal, it would be easier to push the residual to zero than to fit an identity mapping by a stack of nonlinear layers.

These types of shortcut connections allow ResNet to be much deeper than traditional deep networks. In essence, the authors assert that residual connections allow deeper networks (for which training accuracy has fallen off) to more easily choose the exact same parameterization as shallower networks for which the training accuracy was high. Theoretically, the deeper networks would simply have to build identity mappings on top of the shallower networks to get the same results. And thus, the accuracy should at least not drop with more layers.

In real cases, it is unlikely that identity mappings are optimal, but our reformulation may help to precondition the problem. If the optimal function is closer to an identity mapping than to a zero mapping, it should be easier for the solver to find the perturbations with reference to an identity mapping, than to learn the function as a new one. We show by experiments (Fig. 7) that the learned residual functions in general have small responses, suggesting that identity mappings provide reasonable preconditioning.

Unlike other deep learning “tricks” such as batch normalization (BN), residual connections add no additional parameters or computational complexity.

By testing multiple plain networks of varying depth with BN, the authors observe the degradation problem and assert that the cause is not vanishing gradients. They believe that the use of BN is sufficient to counteract the potential issue and also observe that the gradients appear to be healthy. They thus “conjecture that the deep plain nets may have exponentially low convergence rates, which impact the reducing of the training error.”

---

Why does it work?

TLDR; In neural networks, the correlation between the gradients decreases exponentially as the number of layers increases, which makes training difficult. Residual connections slow down this “obliteration of spacial structure.”

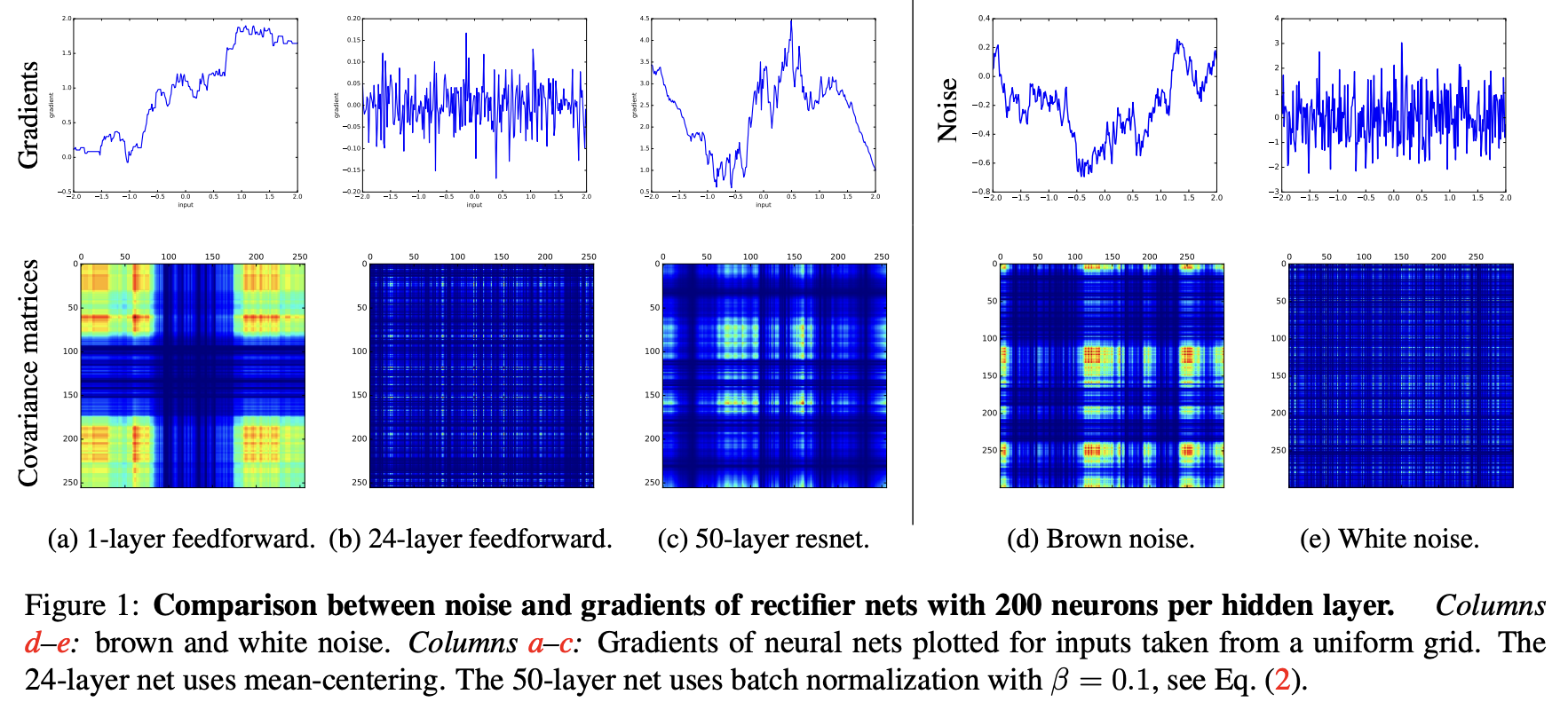
Balduzzi, David, et al describe the shattered gradients problem in their paper titled “The Shattered Gradients Problem: If resnets are the answer, then what is the question?” The authors empirically show that gradients of shallow networks resemble brown noise whereas gradients of deep networks resemble white noise.

They also provide a theoretical explanation for this phenomenon:

Theorem 1 (covariance of gradients in feedforward nets). Suppose weights are initialized with variance ${\sigma }^2=\frac{2}{N}$ following He et al. (2015). Then

1. The variance of the gradient at $x^{(i)}$ is ${\mathcal{C}}^{fnn}(i)=1$.
2. The covariance is ${\mathcal{C}}^{fnn}(i,j)=\frac{1}{2^L}$.

Essentially, they show through theorem 1 that “correlations between gradients decrease exponentially $\frac{1}{2^L}$ with depth in feedforward rectifier networks.”

They build on this observation by asserting that “training is difficult when gradients behave like white noise.”

The shattered gradient problem is that the spatial structure of gradients is progressively obliterated as neural nets deepen. The problem is clearly visible when inputs are taken from a one-dimensional grid, but is difficult to observe when inputs are randomly sampled from a highdimensional dataset.

Shattered gradients undermine the effectiveness of algorithms that assume gradients at nearby points are similar such as momentum-based and accelerated methods (Sutskever et al., 2013; Balduzzi et al., 2017). If $\frac{d{f}_W}{d{n}_j}$ behaves like white noise, then a neuron’s effect on the output of the network (whether increasing weights causes the network to output more or less) becomes extremely unstable making learning difficult.

They then attempt to explain why ResNets may be a solution to the aforementioned problem: “Gradients of deep resnets lie in between brown and white noise.”

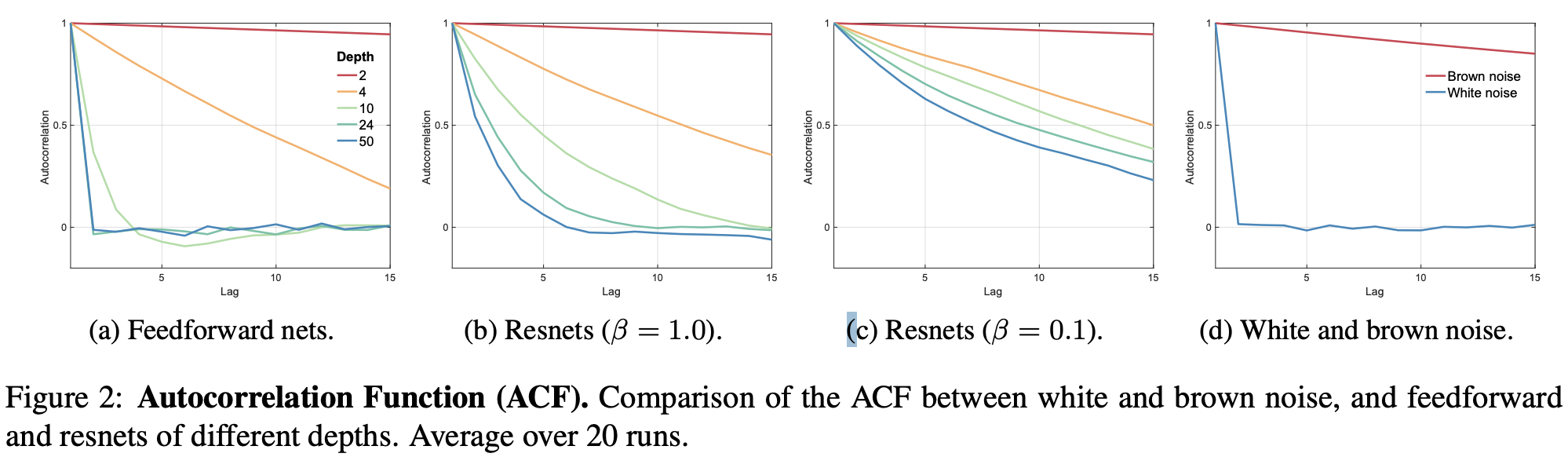
Introducing skip-connections allows much deeper networks to be trained (Srivastava et al., 2015; He et al., 2016b;a; Greff et al., 2017). Skip-connections significantly change the correlation structure of gradients. Figure 1c shows the concrete example of a 50-layer resnet which has markedly more structure than the equivalent feedforward net (figure 1b). Figure 2b shows the ACF of resnets of different depths. Although the gradients become progressively less structured, they do not whiten to the extent of the gradients in standard feedforward networks— there are still correlations in the 50-layer resnet whereas in the equivalent feedforward net, the gradients are indistinguishable from white noise. Figure 2c shows the dramatic effect of recently proposed $\beta$-rescaling (Szegedy et al., 2016): the ACF of even the 50 layer network resemble brown-noise.

They again provide a theoretical explanation:

Theorem 3 (covariance of gradients in resnets with BN and rescaling). Under the assumptions above, for resnets with batch normalization and $\beta$-rescaling

1. the variance is ${\mathcal{C}}_{\beta ,BN}^{res}(i)={\beta }^2(L-1)+1$;
2. the covariance is ${\mathcal{C}}_{\beta ,BN}^{res}(i,j)\sim \beta \sqrt{L}$; and the correlation is ${\mathcal{R}}_{\beta ,BN}^{res}(i,j)\sim \frac{1}{\beta \sqrt{L}}$.

The theorem explains the empirical observation, figure 2a, that gradients in resnets whiten much more slowly with depth than feedforward nets. It also explains why setting $\beta$ near zero further reduces whitening.

Intuitions

From Gemini:

Think of the “correlation of gradients” as a measure of how structured and meaningful the learning signal is. A high correlation is good; a low correlation means the signal is random noise (it’s “whitened” or “shattered”).

• Without Batch Norm (in standard nets): The correlation decays exponentially (like 1/2^L). This is incredibly fast. After just a few layers (L), the signal is essentially gone.
• With Batch Norm (in ResNets): The correlation decays much more slowly, sublinearly (like 1/√L). This allows a meaningful signal to travel through much deeper networks.

Intuitively, gradients whiten because the number of paths through the network grows exponentially faster with depth than the fraction of co-active paths.

The representational power of rectifier networks depends on the number of linear regions into which it splits the input space. It was shown in Montufar et al. (2014) that the number of linear regions can grow exponentially with depth (but only polynomially with width). Hence deep neural networks are capable of far richer mappings than shallow ones (Telgarsky, 2016). An underappreciated consequence of the exponential growth in linear regions is the proliferation of discontinuities in the gradients of rectifier nets.

Proof Strategy. The covariance defines an inner product on the vector space of real-valued random variables with mean zero and finite second moment. It was shown in Balduzzi et al. (2015); Balduzzi (2016) that the gradients in neural nets are sums of path-weights over active paths, see section A3. The first step is to observe that path-weights are orthogonal with respect to the variance inner product. To express gradients as linear combinations of path-weights is thus to express them over an orthogonal basis.

Working in the path-weight basis reduces computing the covariance between gradients at different datapoints to counting the number of co-active paths through the network. The second step is to count co-active paths and adjust for rescaling factors (e.g. due to batch normalization).

References: He, Kaiming, et al. “Deep residual learning for image recognition.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2016. Balduzzi, David, et al. “The shattered gradients problem: If resnets are the answer, then what is the question?.” International conference on machine learning. PMLR, 2017.