ProtoPool

This paper attempts to improve upon ProtoPNet, an interpretable image classification model which identifies parts of an image where it thinks this looks like that prototypical part of some class and it “makes its prediction based on a weighted combination of the similarity scores between parts of the image and the learned prototypes.”

The main innovation of ProtoPool is that instead of assigning a separate set of prototypes to each class, they use a shared pool of prototypes. This significantly reduces the total number of prototypes necessary for training and inference, allows for more interpretability, and reduces the number of “background prototypes.” Another novelty of ProtoPool is the fully differentiable assignment of prototypes to classes which allows for much easier training.

Sharing Prototypes

Recall that ProtoPNet utilizes a “Sep” term in their loss function to make sure prototypes belonging to different classes are well separated in the latent space. However, this means that even semantically similar prototypes (which belong to different classes but are nonetheless semantically similar) may be distant in the latent space. This could result in unstable predictions and is why sharing prototypes is necessary.

Architecture

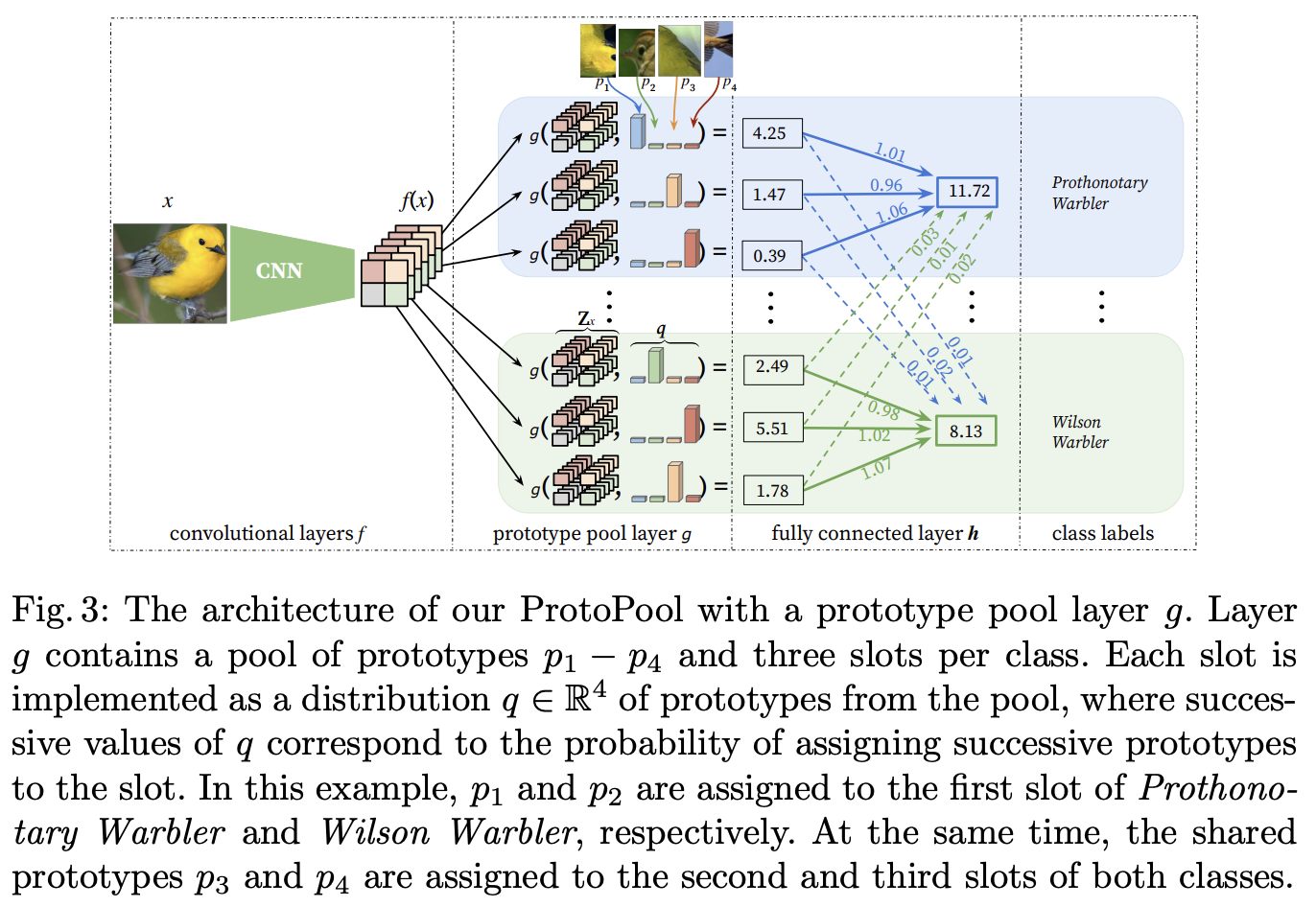The architecture of ProtoPool is very similar to ProtoPNet. There is a convolution layer $f$, prototype pool layer $g$, and a fully connected layer $h$. The most important part of the model is the prototype pool layer. There are $M$ trainable prototypes and $K$ “slots” for each class. Each slot is made up of a probability distribution of all the prototypes available in the pool. The Gumbel-Softmax enforces the notion that each slot should assign a very high probability to one prototype and that different slots corresponding to the same class should not have the same or very similar prototypes. The fully connected layer is initialized in a way that enforces a “positive reasoning process,” i.e. weights between each class c and its slots are initialized to 1 while remaining weights of h are set to 0.

Given an input image $x\in X$, the convolutional layers first extract image representation $f(x)$ of shape $H\times W\times D$, where $H$ and $W$ are the height and width of representation obtained at the last convolutional layer for image $x$, and $D$ is the number of channels in this layer. Intuitively, $f(x)$ can be considered as a set of $H\cdot W$ vectors of dimension $D$, each corresponding to a specific location of the image (as presented in Figure 3). For the clarity of description, we will denote this set as $Z_x=\{z_i\in f(x):z_i\in {\mathbb{R}}^D,i=1,...,H\cdot W\}$. Then, the prototype pool layer is used on each $k$-th slot to compute the aggregated similarity $g_k={\sum }_{i=1}^M{q}_k^i{g}_{p_i}$ between $Z_x$ and all prototypes considering the distribution qk of this slot, where gp is defined below. Finally, the similarity scores (K values per class) are multiplied by the weight matrix wh in the fully connected layer h. This results in the output logits, further normalized using softmax to obtain a final prediction.

In the above paragraph, the $q_k^i$‘s are the probabilities assigned to each prototype $p_i$. The $g_{p_i}$‘s are the similarity scores between the input $x$ and each prototype $p_i$. The authors suggest the following similarity score function: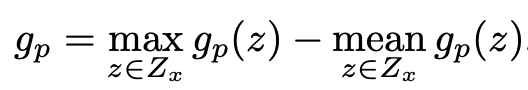

The maximal activation of focal similarity is obtained if a prototype is similar to only a narrow area of the image $x$ (see Figure 2). Consequently, the constructed prototypes correspond to more salient features (according to our user studies described in Section 5), and the gradient passes through all elements of $Z_x$.

---

This architecture allows all the classes to share certain prototypes but also allows each individual class to have its own classes that no other class uses. It accomplishes this by both using a shared pool of prototypes and having a separate set of $K$ “slots” for each class. I’d imagine if the images across the classes were similar enough that they could solely rely on shared prototypes, the “slot” element would be unnecessary, i.e. we could use one global prototype assignment layer. This would simplify the architecture greatly and perhaps speed up training. In interpretability, simplicity is everything.

References: Interpretable Image Classification with Differentiable Prototypes Assignment